🚗 PABD: Accelerating Autonomous Driving Planning via Prior-Aligned Bridge Diffusion
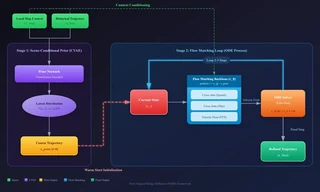 Image credit: Author, 2026
Image credit: Author, 2026Welcome to our project blog 👋
Table of Contents
Overview
Diffusion models have demonstrated superior capability in capturing multi-modal driving behaviors in autonomous driving planning. However, they suffer from a significant bottleneck: high inference latency. Standard diffusion policies typically require 50-100 iterative denoising steps to resolve a clean trajectory from Gaussian noise, making them difficult to deploy in real-time safety-critical systems.
Existing acceleration methods, such as naive warm-starting or discrete anchoring (e.g., k-means), often lead to distribution mismatches known as the “Off-Manifold” problem or fail to capture the continuous nature of open-world driving.
In this project, we introduce Prior-Aligned Bridge Diffusion (PABD), a framework that unifies Scene-Conditional CVAEs with Flow Matching theory. By constructing a straight probability flow between a learned dynamic prior and the ground truth, we minimize the Optimal Transport cost, enabling high-fidelity trajectory generation in as few as 2-3 steps.
The Core Problem
The fundamental challenge lies in the trade-off between generation quality and inference speed.
- The Latency Bottleneck: Standard Stochastic Differential Equation (SDE) approaches require many steps to transform $\mathcal{N}(0,I)$ into a valid trajectory.
- Limitation of Discrete Anchors: Recent works like Diffusion Drive employ discrete anchors. However, discrete clusters fail to capture edge cases in open-world scenarios, leading to mode collapse.
- The “Off-Manifold” Problem: Naive truncation strategies break the Markovian assumption of the forward diffusion process, causing drift errors where the generated trajectory physically violates road constraints.
Our Solution: Prior-Aligned Bridge Diffusion
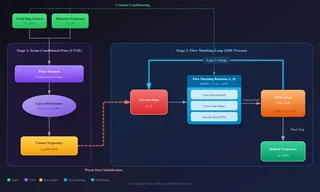
To address these challenges, we propose a two-stage generative framework that replaces the standard SDE with a deterministic Ordinary Differential Equation (ODE) bridge.
Key Innovations
- Scene-Conditional Dynamic Prior (Stage 1): Instead of starting from pure noise or discrete anchors, we train a Conditional Variational Autoencoder (CVAE) as a Prior Network. This encodes local map context ($C_{map}$) and historical trajectories ($x_{hist}$) to generate a coarse, semantically consistent starting point $x_{prior}$.
- Flow Matching Backbone (Stage 2): We define the forward process as a Linear Interpolation (Rectified Flow) between the prior and the ground truth. This creates a constant ideal velocity field that is easier to learn and integrate.
- ODE Solver Acceleration: By starting closer to the target manifold, we drastically reduce the transport cost, allowing the ODE solver to take large steps without significant error.
Technical Implementation
Mathematical Formulation
Unlike standard diffusion which adds noise, we define our process as a bridge between the prior and the ground truth $x_{gt}$:
$$ x_{t}=t\cdot x_{gt}+(1-t)\cdot x_{prior}, \quad t\in[0,1] $$This construction defines a probability flow with a constant ideal velocity field $v = x_{gt} - x_{prior}$. The diffusion backbone $v_{\theta}$ is trained to predict this velocity field by minimizing the flow matching loss:
$$ \mathcal{L}_{flow}=\mathbb{E}_{t,x_{gt},x_{prior}}[||v_{\theta}(x_{t},t,C)-(x_{gt}-x_{prior})||^{2}] $$During inference, we solve the ODE $dX_{t}=v_{\theta}(X_{t},t)dt$ using the Euler method for $N=2\sim3$ steps, initializing from the generated $x_{prior}$.
Theoretical Justification
A critical contribution of this work is the rigorous proof of why PABD achieves acceleration. The global truncation error (GTE) of a first-order numerical ODE solver is bounded by the path’s curvature and velocity magnitude.
Standard diffusion transports mass from Gaussian noise $\mathcal{N}(0,I)$ to data, resulting in a large Wasserstein-2 distance (Transport Cost) and high velocity magnitude. In contrast, our CVAE initialization minimizes this cost:
$$ W_{2}(P_{prior},P_{data})\ll W_{2}(\mathcal{N},P_{data}) \Rightarrow M_{prior}\ll M_{noise} $$Because the convective acceleration term $(v\cdot\nabla)v$ scales quadratically with velocity magnitude, our approach drastically suppresses acceleration. This theoretical guarantee allows the ODE solver to traverse the trajectory with significantly larger step sizes while maintaining a low error bound.
Training Strategy
To ensure stability, we adopt a three-stage curriculum learning strategy:
- Prior Pre-training: Train the CVAE to minimize the ELBO loss, ensuring the prior distribution spatially overlaps with the ground truth manifold.
- Flow Matching Training: Freeze the CVAE and train the diffusion backbone to learn the velocity field.
- Joint Fine-tuning: Unfreeze both networks to allow the prior to adapt to the backbone’s refinement capabilities.
Expected Contributions
Our framework aims to set a new standard for fast, high-quality autonomous planning:
- Theoretical: A rigorous formulation solving the off-manifold sampling issue using Optimal Transport theory.
- Algorithmic: A unified CVAE + Flow Matching architecture enabling valid 2-3 step generation.
- Performance: Empirical validation showing reduced velocity field energy and superior planning metrics (PDMS, L2) compared to current state-of-the-art baselines like DiffusionDrive.

I am currently a Master’s student in Electrical and Computer Engineering at Duke University, maintaining a 4.0 GPA. My research centers on Vision Language Models, Generative AI and Autonomous Driving.
My recent work involves developing StyleVAR, an autoregressive transformer framework for controllable image style transfer. I have also gained industrial research experience at Bosch, where I worked on enhancing VLM grounding capabilities using Reinforcement Learning (GRPO) and data distillation.
Beyond the algorithms, I am an audiophile and a gamer. I enjoy the engineering challenge of building Hi-Res audio systems from scratch—pursuing high fidelity in sound just as I pursue precision in model generation.